「ある値の三分の二」を電卓で計算したい時は「3で割って2を掛ければOK!」です。
(もちろん、電卓以外でも同じように計算できます)
例えば「6万円の三分の二」の場合、
6(万円)÷ 3 × 2 =4(万円)と計算できます。
三分の二(2/3)は、分子(上)÷ 分母(下)、つまり2 ÷ 3=0.66666666666…です。
6万円の三分の二は、6(万円)× 0.6666…と計算してもOKです。
(6万円の場合は、3で割り切れるので、3で割って2を掛けるほうが、計算は楽だと思います)
この記事では、三分の二以外にも、三分の一、四分の一、四分の三、二分の一の計算方法や、それぞれ何%になるのかなどをご紹介します。
電卓での三分の二や、三分の一の計算方法
電卓などで、ある値の「三分の二」「三分の一」を求める方法について解説します。
三分の二は、3等分したうちの2つ
三分の二とは、3等分したうちの2つ分、という意味です。
そのため、3で割って2を掛ければよいことがわかります。
例として、6万円の三分の二を計算する場合で見ていきます。
6(万円)÷ 3 × 2 =4(万円)
- 6万円を三等分すると、6(万円)÷ 3 = 2(万円)
- 2万円のふたつ分だから、2(万円)× 2 = 4(万円)
この他にも、3分の2を計算する方法はあります。
ふたつご紹介しますね。
2を掛けてから3で割ってもよい
6万円の三分の二の計算式は「60000 × 2/3」となります。
そのため、計算する時は、先に60000円に2を掛けてから、3で割ってもOKです。
子供の頃に習った分数の計算です。
6(万円)× 2 ÷ 3 =4(万円)
三分の二は2÷3=0.666…
三分の二(2/3)は、分子(上)÷ 分母(下)、つまり 2 ÷ 3 = 0.66666666666…です。
そのため、0.6666…を掛けてもOKです。
60000(円)× 0.6666… ≒ 40000(円)
三分の二の書き方は?
三分の二の書き方は、以下のようにいくつかあります。
どのように書いてもよいです。
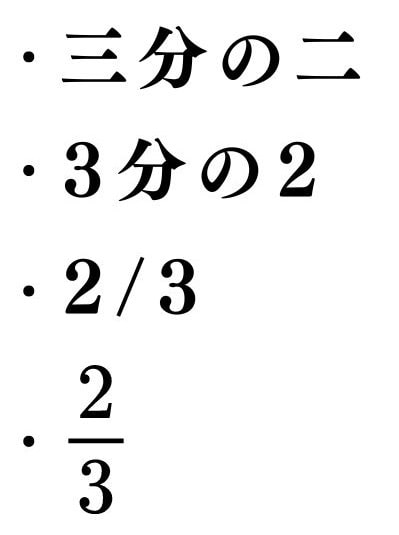
分数を読むときは分母から読みますが、2/3のように書く場合、先に分子から書きます。
ちょっと混乱してしまうかもしれませんが、分子と分母を分ける横線がちょっと斜めになったと思えばわかりやすいでしょう。
三分の二は何%
三分の二を%で表すと、約67%となります。
2/3=2 ÷ 3 = 0.6666…でしたね。
%で表すときは、100を掛けるだけです!
つまり、三分の二は、2 ÷ 3 × 100(%)= 66.6666…(%)≒ 67% となります。
2/3の他の計算例
6万円以外でも、いくつか三分の二の計算をしてみましょう。
紹介した3種類の方法で計算してみました。
例1)一万円の3分の2は?
- 10000(円)÷ 3 × 2 = 6666.66…(円)= 約6667(円)
- 10000(円)× 2 ÷ 3 = 6666.66…(円)= 約6667(円)
- 10000(円)× 0.666…=6666.66…(円)= 約6667(円)
例2)12万円の3分の2は?
- 120000(円)÷ 3 × 2 = 80000(円)
- 120000(円)× 2 ÷ 3 = 80000(円)
- 120000(円)× 0.666…= 80000(円)
例3)25万円の3分の2は?
- 250000(円)÷ 3 × 2 = 166666.66…(円)= 約166667(円)
- 250000(円)× 2 ÷ 3 = 166666.66…(円)= 約166667(円)
- 250000(円)× 0.666…=166666.66…(円)= 約166667(円)
例4)1時間の3分の2は何分?
1時間は60分です。
したがって、
- 60(分)÷ 3 × 2 = 40(分)
- 60(分)× 2 ÷ 3 = 40(分)
- 60(分)× 0.666…= 40(分)
三分の一の計算方法
三分の一の計算方法も同様です。
三分の一とは、3等分したうちの1つ分、という意味です。
そのため、3で割ればよいことがわかります。
6(万円)÷ 3 = 2(万円)
- 6万円を三等分すると、6(万円)÷ 3 = 2(万円)
- 2万円のひとつ分だから、2(万円)× 1 = 2(万円)
3分の2の計算の時のように、他の二つの計算方法も見ていきましょう。
1を掛けてから3で割ってもよい
6万円の三分の一の計算式は「60000 × 1/3」なので、1を掛けてから3で割ってもよいです。
ただ、1を掛けても元の数と変わらないので省略できますね。
そのため、先ほどの計算と同じく3で割るだけでOKです。
三分の一は1÷3=0.3333…
また、三分の一(1/3)は、分子(上)÷ 分母(下)、つまり 1 ÷ 3 = 0.3333…です。
そのため、0.3333…を掛けてもOKです。
60000(円)× 0.3333… ≒ 20000(円)となります。
三分の一は約33%
1/3を%で表す場合は、1 ÷ 3 × 100(%)= 33.3333…(%)です。
約33%となります。
電卓での四分の一や、四分の三の計算方法
続いて、電卓で、四分の一や、四分の三を計算する方法を紹介します。
計算方法は、三分の二で説明した方法と同じです。
こちらも6万円を例に見ていきましょう。
四分の一の計算方法
四分の一とは、4等分したうちの1つ分、という意味です。
そのため、4で割ればよいことがわかります。
6(万円)÷ 4 = 1.5(万円)
- 6万円を四等分すると、6(万円)÷ 4 = 1.5(万円)
- 1.5万円のひとつ分だから、1.5(万円)× 1 = 1.5(万円)
これまでと同じように、他の二つの計算方法も見ていきましょう。
1を掛けてから4で割ってもよい
6万円の四分の一の計算式は「60000 × 1/4」なので、1を掛けてから4で割ってもよいです。
ただ、1を掛けても元の数と変わらないので省略できますね。
そのため、上の計算のように、4で割るだけでOKです。
四分の一は1÷4=0.25
また、四分の一(1/4)は、分子(上)÷ 分母(下)、つまり 1 ÷ 4 = 0.25です。
そのため、0.25を掛けてもOKです。
60000(円)× 0.25 = 15000(円)となります。
四分の一は25%
ちなみに、1/4を%で表す場合は、1 ÷ 4 × 100(%)= 25(%)となります。
四分の三の計算方法
四分の三とは、4等分したうちの3つ分、という意味です。
そのため、4で割って3を掛けばよいことがわかります。
6(万円)÷ 4 × 3 = 4.5(万円)
- 6万円を四等分すると、6(万円)÷ 4 = 1.5(万円)
- 1.5万円の3つ分だから、1.5(万円)× 3 = 4.5(万円)
これまでと同じように、他の二つの計算方法も見ていきましょう。
3を掛けてから4で割ってもよい
6万円の四分の三の計算式は「60000 × 3/4」なので、3を掛けてから4で割ってもOKです。
6(万円)× 3 ÷ 4 = 4.5(万円)
四分の三は3÷4=0.75
また、四分の三(3/4)は、分子(上)÷ 分母(下)、つまり 3 ÷ 4 = 0.75です。
そのため、0.75を掛けてもOKです。
60000(円)× 0.75 = 45000(円)となります。
四分の三は75%
3/4を%で表す場合は、3 ÷ 4 × 100(%)= 75(%)となります。
電卓での二分の一の計算方法
最後に、二分の一の計算方法について解説します。
二分の一の計算方法
二分の一の計算方法も同様です。
二分の一とは、2等分したうちの1つ分、という意味です。
そのため、2で割ればよいことがわかります。
(2等分ということは、つまり半分ということですね)
6(万円)÷ 2 = 3(万円)
- 6万円を二等分すると、6(万円)÷ 2 = 3(万円)
- 3万円のひとつ分だから、3(万円)× 1 = 3(万円)
他の二つの計算方法も見ていきましょう。
1を掛けてから2で割ってもよい
6万円の二分の一の計算式は「60000 × 1/2」なので、1を掛けてから2で割ってもよいです。
ただ、1を掛けても元の数と変わらないので省略できますね。
そのため、2で割るだけでOKです。
二分の一は1÷2=0.5
また、二分の一(1/2)は、分子(上)÷ 分母(下)、つまり 1 ÷ 2 = 0.5です。
そのため、0.5を掛けてもOKです。
60000(円)× 0.5 = 30000(円)となります。
二分の一は50%
1/2を%で表す場合は、1 ÷ 2 × 100(%)= 50(%)となります。
二分の一は、わかりやすいと思います。
まとめ
三分の二は、3等分したうちの2つ分です。
三分の二(2/3)は 0.66666666666…です(約67%)。
三分の二の計算方法には次の3つがあります。
- 3で割って2を掛ける
- 2を掛けて3で割る
- 0.6666…を掛ける
日常生活で、分数計算が求められる場面は多々あります。
例えば「金額の2/3まで補助金が出ます」という時の計算や、全授業の2/3以上の出席が必要な場合の出席回数の計算、年末調整や保険料の計算などでも必要になるかもしれません。
いくつか方法があるので、やりやすい方法で計算してみてくださいね。
